Valve Flow Coefficient (Cv), also known as flow cv, refers to the valve’s flow coefficient: a hydraulic resistance parameter that allows its flow capacity to be measured. During the design of industrial plants, it is one of the key elements for valve selection: calculating the flow cv enables designers to ensure the operation, efficiency, and safety of the entire system.
The Cv coefficient of flow is therefore a key parameter in valve selection, helping designers determine the correct size, opening degree, and design. In fact, if the flow coefficient is smaller than required, this can cause the valve to be undersized, resulting in insufficient fluid, equipment failure, or a greater pressure drop than expected.
On the other hand, a higher flow cv value leads to the installation of larger, oversized valves, resulting in increased costs, as well as higher pressures and velocities that can cause cavitation and possible trim erosion. For this reason, modern industrial plant design software, such as ESApro Head Loss, starting from the 3D model of the system, allows the calculation of pressure losses along a piping line and analysis of the Cv of each valve.
ESAin’s software also automatically derives the sequence of components inserted on the piping line, generates calculation sheets with geometric data, and associates each component with its resistance coefficient.
Let’s find out together how flow coefficient is calculated for each type of fluid and what factors can influence the final value of the coefficient.
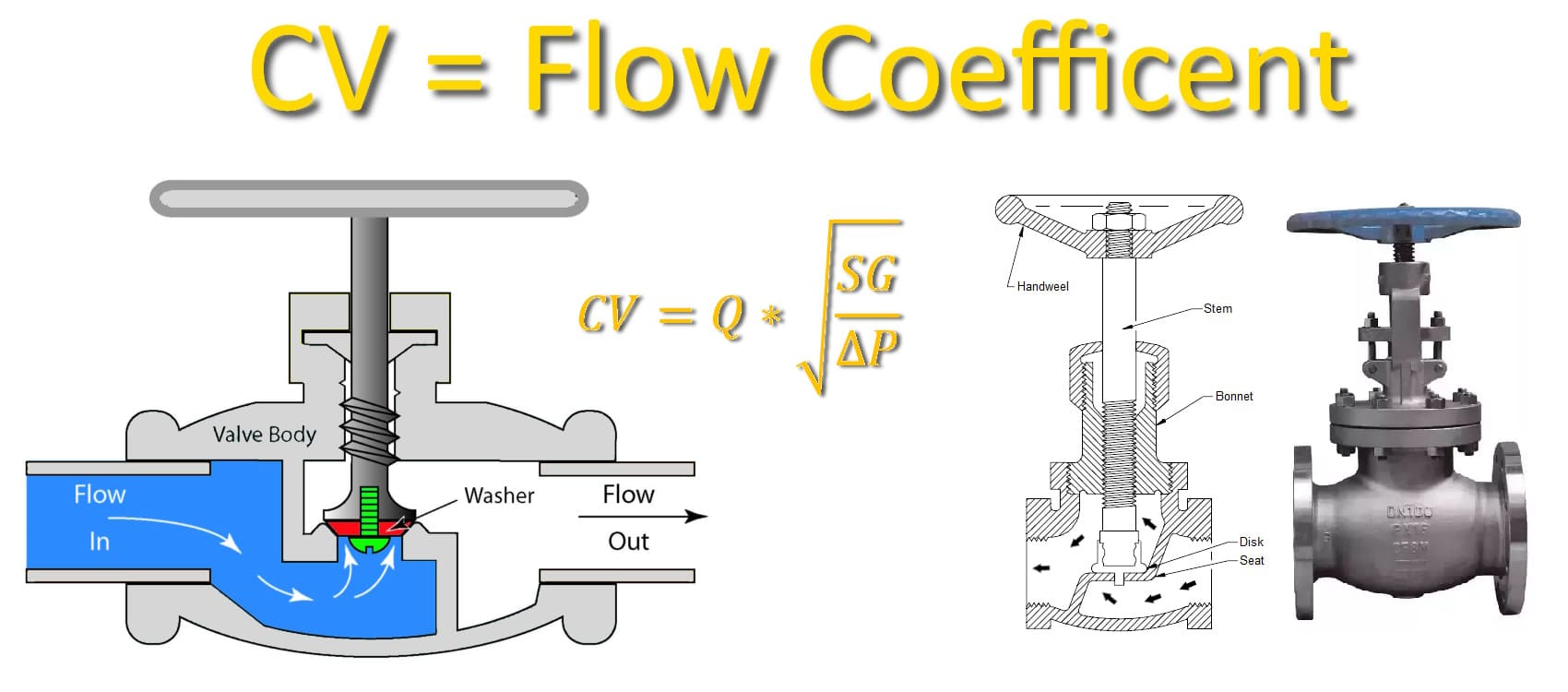
What is Valve Flow Coefficient (Cv)
This parameter is represented in different ways according to the applicable reference standard: the flow coefficient is denoted as “Kv” by European standards, while in the American context it is indicated as “Cv.” The flow cv can also be used for any type of valve, as well as for other hydraulic components in the system, and is influenced by a series of parameters:
- Nominal diameter: as the valve size increases, so do the flow coefficients.
- Type of valve: the coefficient varies depending on the structure of the component used. For example, ball valves generally have a higher valve flow coefficient than globe valves; in the latter type, the Cv can also change depending on the flow control mode, which can be free or throttled.
The value of the valve flow coefficient is generally indicated by the manufacturer in the technical data sheet of the chosen model: those who design industrial plants must therefore calculate the flow cv values with precision, to select the most suitable valves for the type of system they intend to build.
n fact, just like the calculation of the pipe schedule, the Cv flow coefficient definition is essential to ensure the safety of the entire piping line and to prevent problems or malfunctions that could damage the system and the people working within it.
How to calculate flow coefficient Cv
As mentioned, the Cv coefficient of flow is a number that represents a valve’s ability to let fluid pass through it: the higher its value, the greater the flow passing through. This parameter is also influenced by the valve opening: the highest value is recorded when the valve is fully open.
Referring to the American standard, we can define US gal/min and lbf/in² as the units of measurement for the flow factor, but other units of measurement may also be used, such as l/min, Imp gal/min, and lbf/in². The calculation of Cv varies according to the type of fluid, so different formulas can be used for calculating the flow coefficient:
- For liquids. The flow factor is equal to Q*√(SG/ΔP), where Q indicates flow rate (in gallons per minute), SG the specific gravity of the fluid (for water = 1), and ΔP is the pressure drop (in psi). For liquids, we can thus define the Cv coefficient as the volume of water at 60°F that will pass through the valve with a pressure drop of 1 psi.
- For gases. The flow cv is equal to 0.06223Q √[(T *SG)/{Z*(P1² – P2² )}], where Q is the flow rate, P1 and P2 are the upstream and downstream pressures respectively, Z is the absolute temperature, and SG is the specific gravity, which for air is 1.